| sudoku-screenshots | ||
| .DS_Store | ||
| _config.yml | ||
| CNAME | ||
| db.pl | ||
| README.md | ||
INTRODUCTION
A Latin square of order n is an n × n array in which each cell contains a single symbol
from a set S with n elements, such that each symbol occurs exactly once in each row
and exactly once in each column.
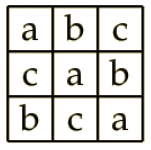
Example:
A Sudoku Latin square is a Latin square of order 9 on the symbol set {1,..., 9} that
is partitioned into 3 × 3 squares, and each square contains all symbols.
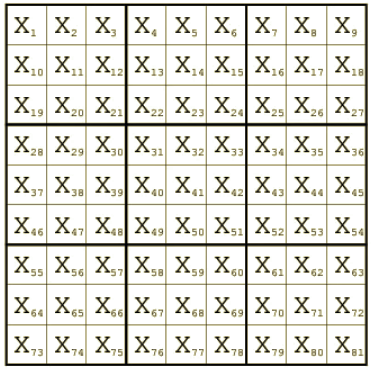
This can also be represented as

This can be further represented as a list of variables:

And we represent the whole sudoku latin square as a list of lists.

So, in total, we have a list of rows.
CLP(FD) CONSTRAINTS
The library clpfd or Constraint Logic Programming over Finite Domains contains a lot
of built-in predicates that are useful for solving the Sudoku puzzle easily.
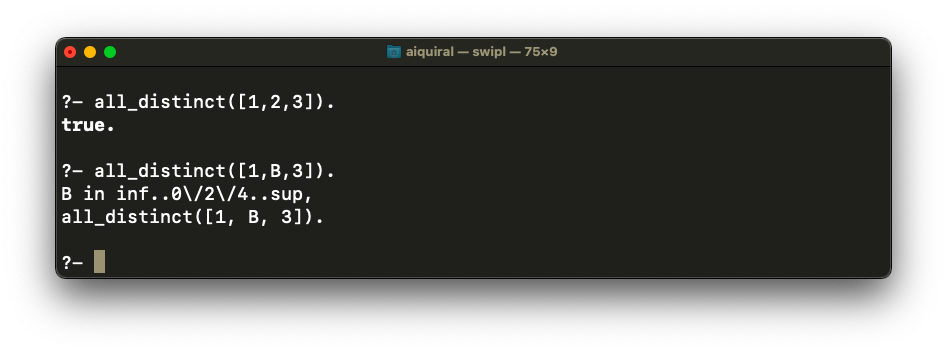
(ins)/2 states the domains of variables in some systems: fd_domain/3, domain/
all_distinct/ or alternatively: all_different/1, fd_all_different. describes a list of different integers
CONSISTENCY TECHNIQUES
all_distinct/1 uses powerful methods from graph theory to prune the search space:
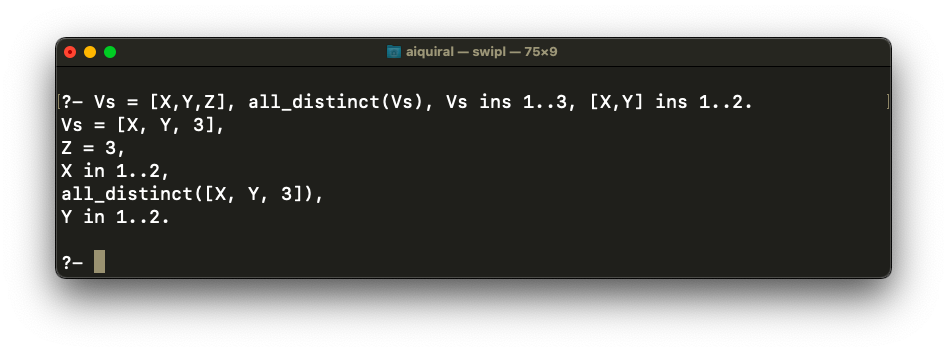
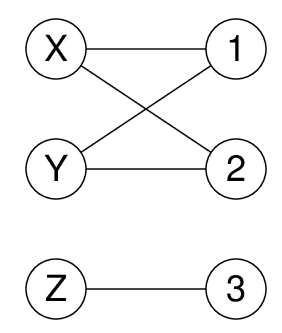
Using the previous example, the following graph states that X can be either 1 or 2, Y
can be either 1 or 2 and Z can be either 1, 2 or 3.
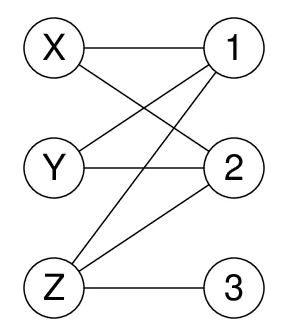
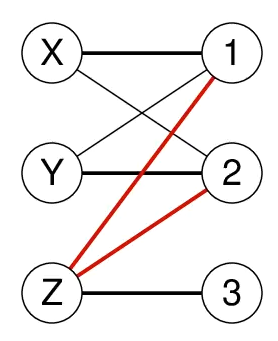
This is a value graph for a set of constraints.
Prolog automatically reasons about this value graph to detect whether there can still
be a solution and also to find out which assignment can not occur in a solution.
PROGRAM
:- use_module(library(clpfd)). % Including clpfd library.
% Defining a sudoku latin square:
sudoku (Rows) :-
% Rows must be a list of length 9.
length (Rows, 9),
%Each of the rows must also be a list of 9.
maplist(same_length(Rows), Rows),
% The concatenation of all elements of this list is the list Vs.
append(Rows, Vs),
Vs ins 1..9,
% We can define the all the elements of each of the rows
% must be purely distinct.
% We can do the following:
% Rows = [Rs1|_], all_distinct(Rs1),
% Rows = [_,Rs2|_], all_distinct(Rs2),
% ...
% But there is a simpler way to do this.
maplist(all_distinct, Rows),
% This states that all_distinct must hold for each of the rows.
% Doing the same with columns.
transpose(Rows, Columns),
maplist(all_distinct, Columns),
% Defining the sub-squares.
Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
square(As, Bs, Cs),
square(Ds, Es, Fs),
square(Gs, Hs, Is).
square([], [], []). % This predicate uses 3 rows.
square([N1,N2,N3|Ns1],
[N4,N5,N6|Ns2],
[N7,N8,N9|Ns3]) :-
all_distinct([N1,N2,N3,N4,N5,N6,N7,N8,N9]),
square(Ns1, Ns2, Ns3).
% Defining different problems.
problem(1, [[_,_,_,_,_,4,_,_,2],
[_,6,_,2,_,_,_,3,_],
[_,8,_,_,_,3,5,_,9],
[_,4,_,_,_,_,1,_,_],
[1,_,_,7,_,5,_,_,_],
[5,_,3,_,_,_,_,_,_],
[_,9,_,3,_,_,_,_,_],
[_,_,4,_,6,1,_,_,_],
[_,_,5,_,_,_,7,_,_]]).
problem(2, [[_,_,9,5,_,_,_,3,7],
[1,3,7,9,_,_,_,5,2],
[2,_,_,_,_,3,6,9,_],
[3,5,2,_,1,_,_,_,6],
[_,_,_,4,5,2,3,_,_],
[_,8,1,_,3,_,2,_,_],
[6,_,3,_,4,_,8,_,9],
[5,2,_,_,_,1,_,6,_],
[_,_,_,3,_,7,_,_,_]]).
problem(3, [[_,5,_,1,_,_,_,_,_],
[2,_,_,5,_,_,6,_,_],
[1,_,_,_,8,_,2,_,_],
[_,8,_,4,3,_,_,_,_],
[_,_,_,_,_,_,_,4,_],
[_,_,_,_,_,7,9,3,2],
[_,4,_,6,7,_,_,_,_],
[_,7,_,_,_,_,_,1,9],
[9,_,_,_,_,8,_,_,_]]).
SOLUTION
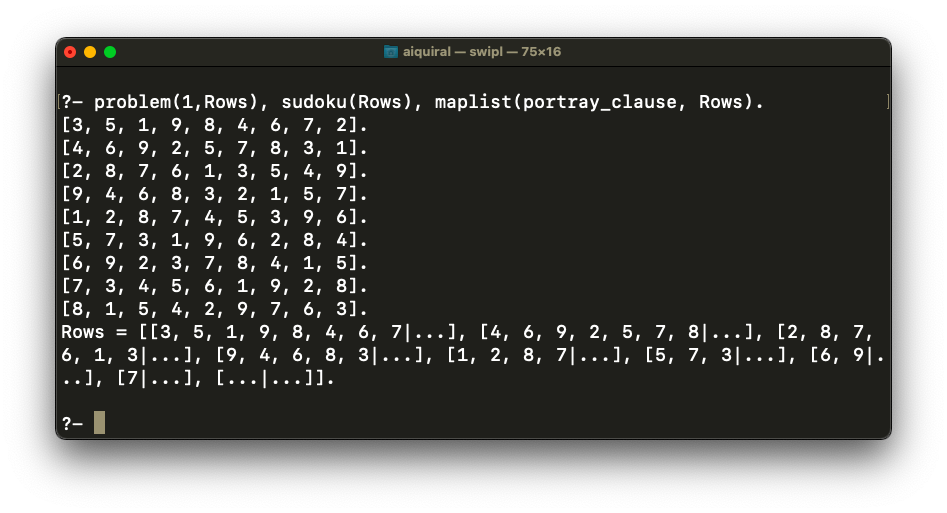
We can get the solution using the following queries:
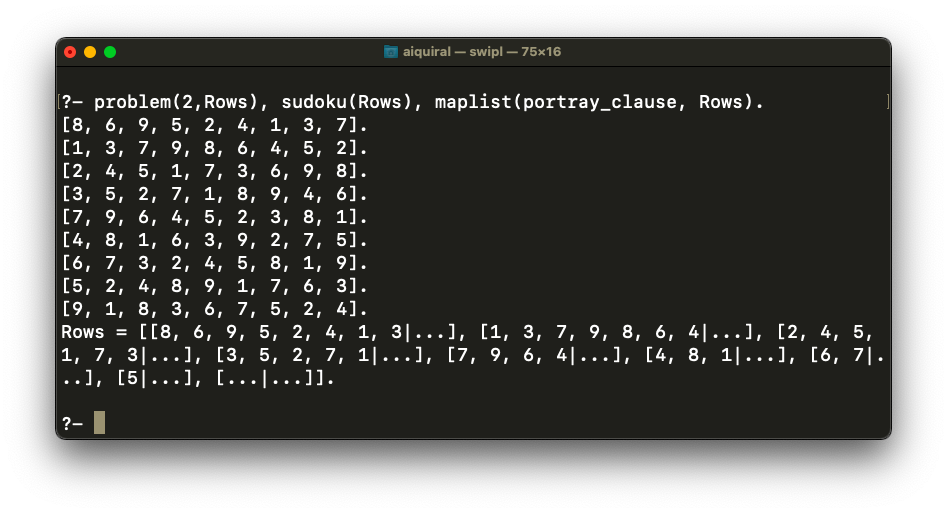
problem(1,Rows), sudoku(Rows), maplist(portray_clause, Rows).
problem(2,Rows), sudoku(Rows), maplist(portray_clause, Rows).
problem(3,Rows), sudoku(Rows), maplist(portray_clause, Rows).
ANOTHER EXAMPLE
Following is the step by step method of how prolog solves the Sudoku puzzle using
intelligent constraint propagation.
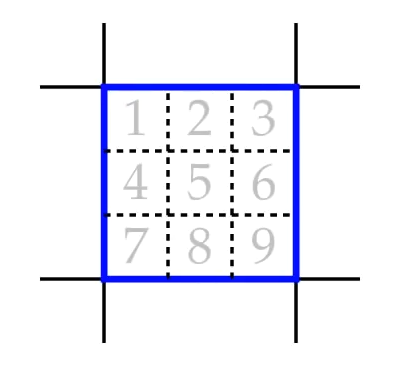

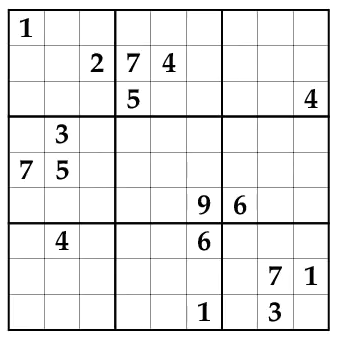
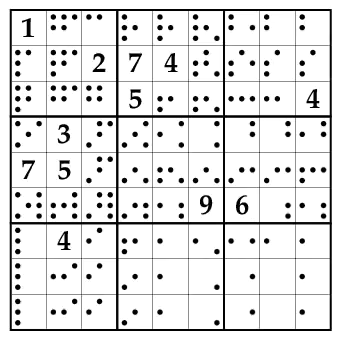
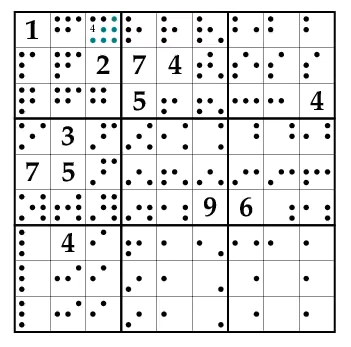
Inconsistent values are indicated by small dots. Black dots represent “obvious”
propagation, whereas, blue dots represent “intelligent” propagation.